SLAM问题中的李群和李代数

0.动机

在探讨李群李代数之前，我们先思考一个问题。为什么要在SLAM中引入李群和李代数？答：为了优化过程中的求导。

先来看一下最简单的最小二乘问题：

$\min _{x} \frac{1}{2}\|f(x)\|_{2}^{2}$

简单来说，我们要找到一个 $x$，使函数达到极值，换成SLAM的情景，就是我们要找到一个位姿，让它最“合理”，我们一般定义观测与实际数据的误差，尽量使其最小化。

还是先从简单的例子开始考虑，如果函数是像 $f(x)=x^2$ 这种很简单的形式，那么很容易通过求导数为0点，通过解析形式求出结果。然而一旦函数变得复杂，无法以解析形式求解，就需要用迭代的方式进行求解了：

先给定一个初始值 $x_0$
寻找一个增量 $\Delta x$，使$ \left|f\left(x_{i}+\Delta x\right)\right|_{2}^{2}<\left|f\left(x_{i}\right)\right|_{2}^{2}$ （其实就是寻找函数降低的方向)
若 $\Delta x$ 足够小，则停止迭代
否则令 $x_{i+1}=x_{i}+\Delta x$ ，继续迭代

问题就出在第二步上，求取函数的下降方向就需要对函数求导，回想一下导数的定义，再看看第二步做了什么，怎么都绕不开一件事 $x_{i+1}=x_{i}+\Delta x$ ，然而问题是，连续变换时，旋转矩阵R更新的方式是不断左乘新的旋转矩阵，而不是加。

回顾一下旋转矩阵R的性质：它是一个行列式为1的正交矩阵。即它的逆就是它自身的转置 $R^{-1}=R^{T}$ 。一个旋转矩阵加另一个旋转矩阵，得到的那一坨东西并不一定还能满足旋转矩阵（特殊正交群$SO(3)$）的性质，我们管这个叫：

特殊正交群对加法不封闭，但把其映射成李代数之后，向量的加法是封闭的，从而解决求导这个问题

1. 一些概念

1.1 什么是群？

旋转矩阵和乘法就构成了旋转矩阵群，但旋转矩阵和加法不能构成群，因为不满足封闭性，旋转矩阵本身具有约束$\left\{R \in \mathbb{R}^{n \times n}\left|R \times R^{T}=I\right| \operatorname{det}(R)=1\right\}$，两个旋转矩阵相加$R1+R2$的结果就不能满足上述约束了，但$R1R2$可以满足，此外，旋转矩阵还满足结合律：$R1R2=R2*R1$，还有幺元是单位矩阵$I$，也有逆矩阵满足R乘以R的逆等于幺元（单位阵）。我们在SLAM里最常说的有两个，一个是特殊正交群$SO(3)$，也就是旋转矩阵群，还有特殊欧氏群$SE(3)$，也就是变换矩阵群，3代表是三维的。

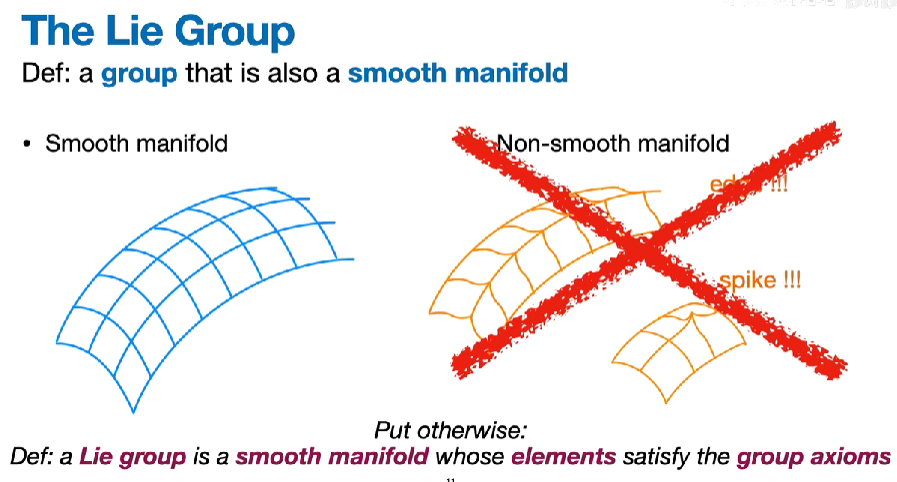
1.2 什么是李群？

李群的定义是指连续光滑的群，比如我们前面说的旋转矩阵群$SO(3)$，你可以想象你拿个杯子就可以在空间中以某个支点连续地旋转它，所以$SO(3)$它就是李群。如果你一般旋转一边移动它，也是连续的或者说光滑的运动，所以变换矩阵群$SE(3)$也是李群。

1.3 什么是李代数？

先上结论：李代数对应李群的正切空间，它描述了李群局部的导数。

通过一系列推导，我们可以得到旋转矩阵的微分是一个反对称矩阵左乘它本身

$\dot{\mathbf{R}}(t)=\phi(t)^{\wedge} \mathbf{R}(t)=\left[\begin{array}{ccc} 0 & -\phi_{3} & \phi_{2} \\ \phi_{3} & 0 & -\phi_{1} \\ -\phi_{2} & \phi_{1} & 0 \end{array}\right] \mathbf{R}(t)$

上式是一个关于R的微分方程，并且 $R(0)=I$ ，解得：

$\boldsymbol{R}(t)=\exp \left(\phi_{0}^{\wedge} t\right)$

于是我们有了一个向量 $\phi$ ，反应了$R$在局部的导数关系，实际上 $\phi $ 正是特殊正交群对应$SO(3)$的李代数 $\mathfrak{s o}(3)$

旋转矩阵特殊正交群 $SO(3)$ 对应的李代数 $\mathfrak{s o}(3)$ 的元素是实数域的三维向量（三维反对称矩阵)

李代数的数学定义：$\mathfrak{s o}(3)=\left\{\phi \in \mathbb{R}^{3}, \Phi=\phi^{\wedge} \in \mathbb{R}^{3 \times 3}\right\}$

$\mathfrak{s o}(3)$ 与 $SO(3)$的关系由指数映射给定： $\boldsymbol{R}(t)=\exp \left(\phi_{0}^{\wedge} t\right)$

下面我们来探讨这个指数映射的含义。

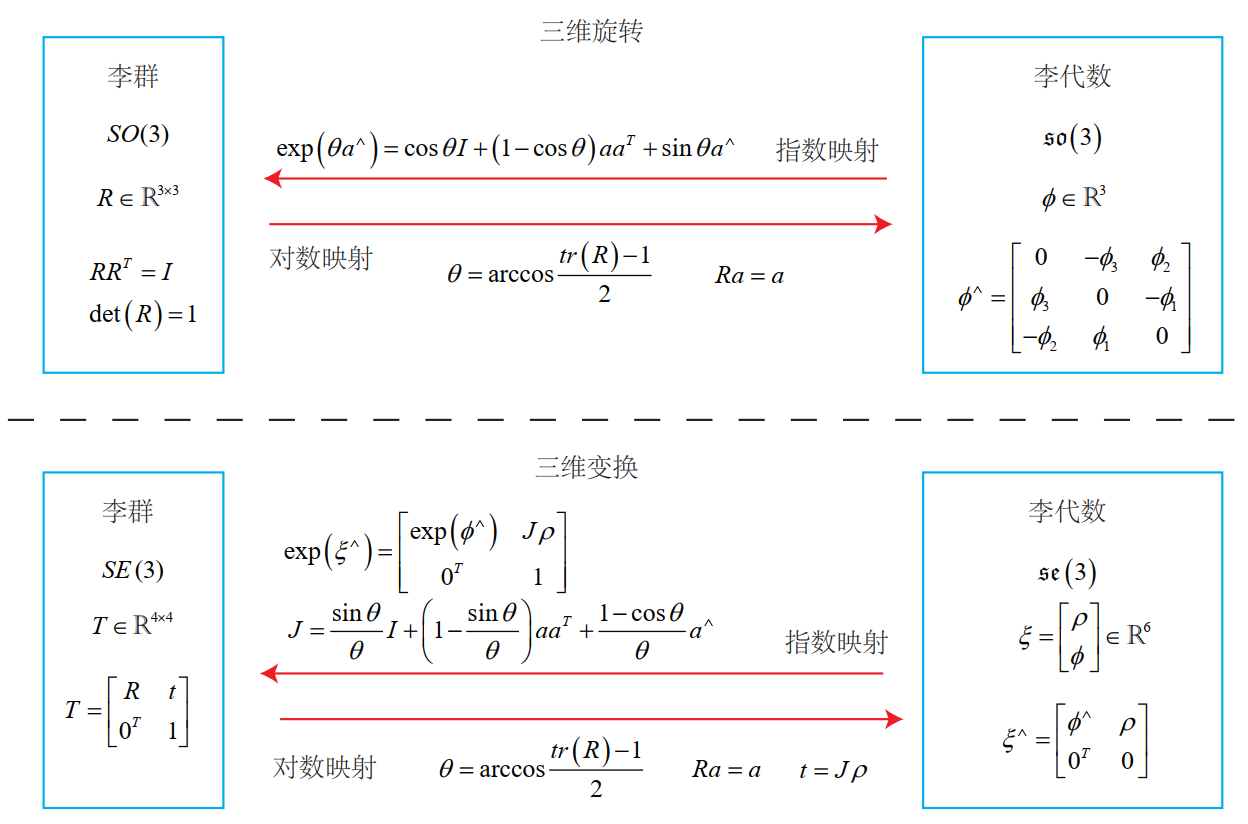
2. 指数和对数映射

2.1 SO(3)上的指数映射

如何计算$\exp \left(\phi_{0}^{\wedge} t\right)$?

任意矩阵的指数映射可以写成一个泰勒展开,但是只有在收敛的情况下才会有结果，其结果仍是一个矩阵。比如对于矩阵 $A$：

$\exp (A)=\sum_{n=0}^{\infty} \frac{1}{n !} A^{n}$

同样的，对于旋转矩阵$R$：

$R=\exp \left(\phi^{\wedge}\right)=\sum_{n=0}^{\infty} \frac{1}{n !}\left(\phi^{\wedge}\right)^{n}$

由于 $\phi$ 是一个三维向量，我们可以用它的模长 $\theta$，和表示方向的单位向量 $a$来表示，即 $\phi=\theta a$，并且会有下面两个性质：

$a^{\wedge} a^{\wedge}=a a^{T}-I \\ a^{\wedge} a^{\wedge} a^{\wedge}=-a^{\wedge}$

这两个式子提供了处理$a^{\wedge}$高阶项的方法，于是上面的指数映射可以写成

最后推导出的结果和罗德里格斯公式一模一样，这下就全说通了，旋转矩阵特殊正交群 $SO(3)$ 对应的李代数就$\mathfrak{s o}(3)$ 是旋转向量组成的空间。如果把旋转角度固定在$±π$之间，那么$SO(3)$和$\mathfrak{s o}(3)$ 的元素是一一对应的。旋转矩阵的导数可以由旋转向量指定，指导着如何在旋转矩阵中进行微积分运算。